ফারাও আমাসিস। আহ্‌, কী দূরদর্শী প্রতাপান্বিত সম্রাটই না ছিলেন তিনি! বয়স হয়েছিল বেশ, অন্তিম শয়ানে তখন, তারপরও রণকৌশল সাজিয়ে গেছেন তিনি, রাজধানী মেমফিসের চারপাশে গড়ে তুলেছেন কঠিন প্রতিরক্ষাবেষ্টনী। দক্ষিণ-পশ্চিম আনাতোলিয়া'র (Turkey) কারিয়া এবং গ্রিস থেকে ভাড়াটে সৈন্য এনে শক্তিশালী করে তুলেছিলেন সেনাদল, মিত্রতার বন্ধনে আবদ্ধ করেছিলেন সামোসের পলিক্রেটিজকে, যাতে পলিক্রেটিজের বিশাল নৌবহর গাজা থেকে পেলুসিয়াম (Pelusium) পর্যন্ত সঙ্কীর্ণ মরুপথটিতে অরক্ষিত পার্সি বাহিনীর উপর শাম সাগর (Syrian Sea) থেকে ভয়ঙ্কর আক্রমণ চালায়।

যুদ্ধ শুরু হবার কিছু দিন পূর্বে বিশ্বাঘাতকতা করে পলিক্রেটিজ। ক্যাম্বাইসিজের পক্ষে যোগ দেয় তার নৌবহর, বিনা বাধায় পার্সি সৈন্যদল পশ্চিম দিকে অগ্রসর হয়ে পৌঁছে যায় পেলুসিয়াম উপসাগরের তীরে। আর এ সময় মারা যান বৃদ্ধ আমাসিস, সিংহাসনে আরোহণ করেন সামতিক—সে কেবল কয়েক মাসের জন্য। পেলুসিয়ামে পরাজিত হয় মিশরবাহিনী, ক্যাম্বাইসিজ অগ্রসর হতে থাকেন আরো পশ্চিমে, হেলিওপলিসের পতন ঘটিয়ে পৌঁছে যান রাজধানী মেমফিসের সদর দরজায়। কয়েক মাস অবরোধের পর ভেঙে পড়ে মেমফিস।

পারস্যরাজ আমাকে বন্দি করে ব্যাবিলনে (Babylon) নিয়ে আসেন, কিন্তু রহস্যময়ভাবে মুক্তভাবে সেখানে চলাচল করতে দেন। অপ্রত্যাশিত সুযোগটি আমি কাজেই লাগাই জ্ঞান সাধনায়—প্রাচ্যদেশীয় জ্ঞানীদের (magi) কাছে দীক্ষালাভ করি অতিন্দ্রীয় শাস্ত্রে, আয়ত্ত করি ক্যালডীয় (Caldean) পুরোহিতদের ধর্মাচার, অর্জন করি নক্ষত্র-অবলোকনকারীদের (star-gazer) গণিত ও জ্যোতির্জ্ঞান। সমকোণী ত্রিভুজ নিয়ে এদেরও ছিল সুতীব্র আকর্ষণ যা আমাকেও তীব্র আলোড়িত করে।

আনুমানিক ১৮০০-১৬০০ খ্রিস্টপূর্বাব্দের একটি ব্যাবিলনীয় শিলাখণ্ড যেখানে কীলক-লিখনের (cuneiform) সাহায্যে ২-এর বর্গমূলের মান ৬০-ভিত্তিক (sexagesimal) পদ্ধতিতে নির্ণয় করা হয়েছে; দশমিক পদ্ধতিতে রূপান্তর করলে বর্গমূলটির মান দশমিকের পর ৫-ঘর পর্যন্ত সঠিক হয়। সৌজন্যে, উইকিপিডয়া

এক যুগ কাটাই আমি ব্যাবিলনে। পারস্যরাজ ক্যাম্বাইসিজ ও গ্রিক স্বৈরাচারী (tyrant) পলিক্রেটিজের মৃত্যু হয় ইত্যবসরে, ফলে সামোস ফিরে আসি আমি। তারপর ক্রিট দ্বীপে কিছু দিন আইনশাস্ত্র অধ্যয়ন করে আবার সামোসে ফিরে একটি বিদ্যালয় চালু করার মনঃস্থির করি।

আহ্‌, সামিয়ানবাসীরা ছিল খুব ব্যস্ত, বিদ্যাশিক্ষার মতো অগুরুত্বপূর্ণ কাজে তাদের সময় ছিল অপ্রতুল। সামগ্রিক বিবেচনা করে চলে আসি ক্রোটন, এখানেই আদিষ্ট আমি, আর সব দার্শনিকের মতো, যারা শেষ নিঃশ্বাস ত্যাগ করেন দূরদেশে। তবে সামোসে পেয়েছি আমি নক্ষত্র এক, তোমাদেরই একজন সে, তোমাদের মতোই আলোকিত, প্রিয় ফিলোক্রেটজ।

"এ-ই হচ্ছে আমার গল্প, হে স্বর্গীয় আলোর দিশারীগণ, হে নির্বাচিত অভিমন্ত্রিতগণ।" পীথাগোরাস শেষ করেন তাঁর কাহিনী, সসম্ভ্রমে সবাই তাকায় ফিলোক্রেটজের দিকে।

সূর্য ডুবে গেছে পশ্চিমাকাশে, ধীরে ধীরে শীতল হয়ে উঠে ভূমধ্যসাগরীয় রাত। "জগতের সবই সংখ্যা, পূর্ণসংখ্যা, যাদের রয়েছে বাস্তব, স্বকীয় অস্তিত্ব।" রহস্যময়ভাবে বলে উঠেন পীথাগোরাস। "সংখ্যা-ই জীবন, সংখ্যা-ই মরণ, সংখ্যা গড়েছে জগত-সংসার। মহাবিশ্বের সবকিছুই পূর্ণসংখ্যায় পরিমাপযোগ্য (commensurable), এমনকি শরীর বলো, আত্মা বলো, ন্যায়বিচার বলো, সবই সংখ্যা।

যেকোনো দুটি সংখ্যাকে তোমরা সর্বদা সুবিধামতো তৃতীয় একটি ক্ষুদ্রতর সংখ্যার পূর্ণ গুণিতক আকারে প্রকাশ করতে পার। যেমন ধরো, ক্রোটনের বাজার থেকে ৫ ড্রাকমা ২ অবোলি দিয়ে কিছু জলপাই কিনলে তুমি, সম পরিমাণ জলপাই কিনলে সামোস থেকে ৪ ড্রাকমা ৪ অবোলি দিয়ে। তাহলে অবোলি হিসেবে তুমি পেলে দুটি সংখ্যা:
৩২ [অবোলি] ও ২৮ [অবোলি], যেহেতু ১ ড্রাকমা=৬ অবোলি।

এখন তুমি যদি একটি ক্ষুদ্রতর সংখ্যা, ১৬ [অবোলি] নাও, তাহলে মূল সংখ্যা দু'টি কিন্তু পরিপূর্ণ বিভাজ্য তথা পূর্ণ গুণিতক হচ্ছে না, কারণ ৩২÷১৬=পূর্ণ সংখ্যা, কিন্তু ২৮÷১৬=পূর্ণ সংখ্যা নয়।

এবার তুমি আরেকটু ক্ষুদ্রতর সংখ্যা নিয়ে চেষ্টা কর: ধরো, ১৪। না, এবারও দুটি পূর্ণ গুণিতক হচ্ছে না। কিন্তু এভাবে ক্ষুদ্রতর সংখ্যাটি কমিয়ে যেতে থাক, এক সময় দেখবে সেটি ৪ ধরলে দুটি সংখ্যাই পূর্ণ বিভাজ্য হচ্ছে: ৩২÷৪=৮, ২৮÷৪=৭। ৪ হচ্ছে ৩২ ও ২৮-এর সাধারণ পরিমাপক (common measure)।

আবার তুমি যদি ড্রাকমা হিসেব করো, তাহলে সংখ্যা দুটি:
৫ ও ১/৩ [ড্রাকমা] এবং ৪ ও ২/৩ [ড্রাকমা]।

এখন তুমি যদি ক্ষুদ্রতর সংখ্যাটি নাও ১/৩, তাহলে আগের মতো ভাগফল হিসেবে পাচ্ছ দুটি পূর্ণ সংখ্যা:
(৫ ও ১/৩)÷১/৩=১৫ ও ১=১৬
(৪ ও ২/৩)÷১/৩=১২ ও ২=১৪

জ্যামিতিকভাবে বললে, ৩২ ও ২৮ যদি দুটি রেখাংশ হয়, তাহলে ৪ মাপের রেখাংশটি তাদের সাধারণ পরিমাপক। এভাবে ২, ১, ১/২, ১/৪... প্রভৃতিও তাদের সাধারণ পরিমাপক হবে।

আবার ৫ ও ১/৩ এবং ৪ ও ২/৩ দুটি রেখাংশ হলে, তাদের সাধারণ পরিমাপক হবে ১/৩, ১/৬, ১/৯...এসব মানের রেখাংশ।


এভাবে ক্ষুদ্রতর সংখ্যাটি যত ক্ষুদ্র নেবে, এক সময় না এক সময় সেটি দিয়ে মূল সংখ্যাদ্বয়কে ভাগকরলে ভাগফল হিসেবে পূর্ণ সংখ্য পাবেই— মহাবিশ্বের সবকিছুই পূর্ণ সংখ্যায় পরিমাপযোগ্য।

"না, এ সত্য নয়, জগতের সবকিছুই এভাবে পূর্ণ সংখ্যায় প্রকাশযোগ্য নয়। অনেক সংখ্যাযুগল আছে দুনিয়ায় যাদের এরূপ তৃতীয় কোনো সাধারণ পরিমাপক পাওয়া যাবে না, তা যত চেষ্টাই করাই হোক, আর পরিমাপকটি যত ক্ষুদ্রাতিক্ষুদ্রই নেয়া হোক না কেন।

আতঙ্কে শিউরে উঠল ভ্রাতৃগোষ্ঠির সদস্যগণ। প্রখর রৌদ্রোজ্জ্বল দিনে ভয়ানক বজ্রপাতেও এতটা চমকে উঠত না তারা। গুরুর সামনে উচ্চকণ্ঠ হয় না তারা, তাঁর শিক্ষাকে অস্বীকার করা তাদের ভয়ানক দুঃস্বপ্নেরও অতীত; আর এ তো স্পষ্ট বিদ্রোহ, ভ্রাতৃগোষ্ঠির বিশ্বাসের মূলে কুঠারাঘাত, তাদের সামগ্রিক জীবনাচারণকে অস্বীকার। কে সে দুরাত্মা, পাপিষ্ঠ! আক্রোশে ফেটে পড়তে উন্মুখ ভ্রাতৃগোষ্ঠির সদস্যগণ।

"কে, কে বলেছে এ কথা?" কঠোর থমথমে মুখে প্রশ্ন করেন পীথাগোরাস।
"আমি, হিপ্যাসাস।" মেটাপানটামের (Metapontum) যুবকটি বলে। গত কয়েক দিন অস্থির সময় কেটেছে। আবিষ্কারটির ভয়ঙ্করতায় প্রথমে স্তম্ভিত হয়ে গিয়েছিল সে, কেঁপে উঠেছিল তার অন্তরাত্মা। তারপরও নানা ভাবে পরীক্ষা করে দেখেছে সে—না, সে-ই ঠিক, পীথাগোরাসের সংখ্যাই জগতের সব সংখ্যা নয়। শেষ পর্যন্ত সহ্য করতে না পেরে উচ্চারণ করেই ফেলেছে সত্যটির কথা।
"তুমি জান কী উচ্চারণ করেছে তুমি? এর কী প্রমাণ আছে তোমার কাছে? প্রমাণ করতে না পারলে তার পরিণতি সম্পর্কে ধারণা আছে?" পীথাগোরাস দৃঢ়কণ্ঠে বলেন।
"হ্যাঁ, প্রমাণ আমি করতে পারব। আপনার সমকোণী ত্রিভুজেই লুকিয়ে আছে তা।" ধীরে ধীরে আত্মবিশ্বাস বাড়তে থাকে হিপ্যাসাসের।
"উঠে এসো এখানে, প্রমাণ কর।"

ভীড় সরিয়ে সেমিসার্কেলে উঠে হিপ্যাসাস। নানা রঙের বালি ও নূড়িপাথর নিয়ে দাঁড়িয়ে আছে একজন সহকারী। মাটিতে একটি বর্গক্ষেত্র আঁকে হিপ্যাসাস, তারপর নীল বালি ছিটিয়ে রঙিন করে তার বাহুগুলো, আর একটি সবুজ কর্ণ তৈরি করে।
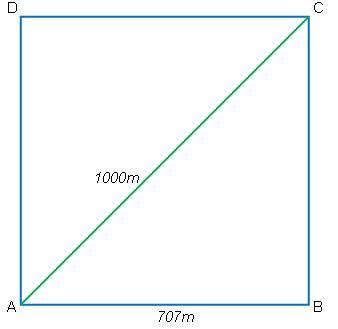
"আপনার কথামতো বাহু-রেখাংশ AB এবং কর্ণ-রেখাংশ AC পরস্পর পরিমাপযোগ্য (commensurable), অর্থাৎ তৃতীয় আরেকটি ক্ষুদ্রতর রেখাংশ তাদের উভয়কে পূর্ণ সংখ্যায় ভাগ করতে পারবে, তাই না?" প্রশ্ন করে হিপ্যাসাস।


"হ্যাঁ, তাই।" ক্ষোভ নিয়ন্ত্রণ করে বলেন পীথাগোরাস, স্পষ্টতই এ ধরণের আচরণ, বিশেষ করে শিষ্যদের কাছ থেকে, একেবারে অকল্পনীয়।
"ধরে নেই, তৃতীয় সেই ক্ষুদ্রতর রেখাংশটির মান m। অতএব, AB ও AC উভয়ে m-এর সাপেক্ষে পরিমেয়, যেখানে m হতে পারে অত্যন্ত ক্ষুদ্র একটি সংখ্যা। বোঝার সুবিধার্থে ধরে নেই, AC=1000m, AB=707m, যদিও পরে আমরা দেখব আমার পদ্ধতিতে 1000 বা 707-এর কোনো ভূমিকা নেই।"
বর্গের কর্ণ যদি ১০ হস্ত হয়, বাহু তার মোটামুটি ৭ হস্ত; ১০০০ হলে মোটামুটি ৭০০, মনে মনে হিসেব করেন পীথাগোরাস। "ঠিক আছে।" বলেন তিনি।

"এবার কর্ণ AC থেকে AB-এর সমান করে AB1 অংশ কেটে নেই। CB1 কে বাহু ধরে আরেকটি বর্গ আঁকি।" বর্গক্ষেত্রটিকে হিপ্যাসাস এবার লালচে বালি দিয়ে স্পষ্ট করেন। পিনপতন নীরবতা সেমিসার্কেলে, কী একটা আঁচ করার চেষ্টা করছেন পীথাগোরাস, কপালে বয়সরেখাগুলোতে ভাঁজ পড়তে শুরু করছে।


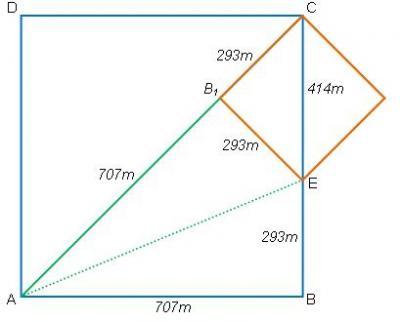
"এখন ছোট বর্গের বাহু, CB1=1000m-707m=293m (=EB1)।
ত্রিভুজ ABE এবং ত্রিভুজ AB1E সর্বসম, কারণ এরা সমকোণী ত্রিভুজ যেখানে দুটি করে বাহু সমান: AB=AB1, AE সাধারণ বাহু।
ফলে EB1=EB=293m, এবং
ছোট বর্গের কর্ণ, CE=707m-293m=414m।
অতএব আমরা পাচ্ছি, ছোট বর্গের বাহু ও তার কর্ণ পরস্পর m-এর সাপেক্ষে পরিমাপযোগ্য।" হিপ্যাসাস একটি বিরতি নেন।

মৃদু গুঞ্জন উঠে সেমিসার্কেলের চারপাশে, এ-তো ঠিকই আছে, সমস্যা কোথায়! হিপ্যাসাস আবার তার চিত্রে মনোযোগ দেয়, CE রেখাংশ থেকে CB1 এর সমান করে CB2 অংশ কেটে নিয়ে আগের মতো ক্ষুদ্রতর একটি বর্গক্ষেত্র অঙ্কন করে, এবারেরটি বেগুনি বর্ণের।

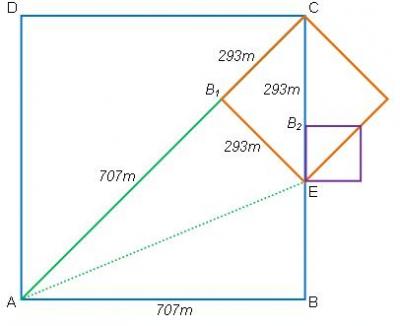
"আগের মতোই আমরা বলতে পারি, বেগুনি বর্গের বাহু এবং তার কর্ণও m-এর সাপেক্ষে পরিমাপযোগ্য, তা m-এর যত গুণিতকই হোক না কেন? তবে আগের বর্গদুটোর চেয়ে এখানে গুণিতকের মান কম হবে, তাই না?" হিপ্যাসাস প্রশ্ন করে।
"হ্যাঁ।" পীথাগোরাস সায় দেন, স্বর তার ক্ষীণ, যুক্তিশাস্ত্রের কোন শাখা দিয়ে হিপ্যাসাস অগ্রসর হচ্ছে, তা ধরতে পেরেছেন তিনি।
"এভাবে m-এর সাপেক্ষে কর্ণ ও বাহুতে গুণিতকের মান কমতে থাকবে। আমি ক্ষুদ্র থেকে ক্ষুদ্রতর বর্গ এঁকে যেতে থাকব, এক সময় এমন এক বর্গ পাব যার বাহু ও কর্ণ m-রেখাংশটির চেয়েও ছোট হয়ে যাবে, ফলে বাহু ও কর্ণ m-এর সাপেক্ষে আর পরিমাপযোগ্য হবে না।"

খানিক থেমে আবার বলে হিপ্যাসাস, "এখন কথা হলো m কত ছোট হতে পারে। আমি সুবিধার জন্য m-কে এমন ধরেছি যে প্রথম বর্গের কর্ণ 1000m ও বাহু 707m হয়। কিন্তু m যত ক্ষুদ্রই হোক না কেন, তা নির্দিষ্ট দৈর্ঘ্যের হবে, কিন্তু আমি এভাবে অসীম সংখ্যক ক্ষুদ্রতর বর্গ আঁকতে পারব, যখন বর্গের বাহু নির্দিষ্ট mটি থেকে এক সময় ছোট হবে।"

"অতএব, যুক্তিশাস্ত্রের রিডাকশিও এড অ্যাবসার্ডাম (reductio ad absurdum) এর ব্যাতিরেকী প্রমাণের (proof by contradiction) মাধ্যমে আমি প্রমাণ করলাম, এক সময় এমন বর্গ আঁকাও সম্ভব যার বাহু ও কর্ণ কোনোভাবেই সাধারণ কোনো পরিমাপকের সাপেক্ষে পরিমেয় নয়! কিন্তু এ তো স্ববিরোধী কথা, কারণ সকল বর্গেরই কর্ণ ও বাহু একই আনুপাতিক সম্পর্কে থাকার কথা।
তার মানে বর্গের বাহু ও কর্ণ আসলেই কখনো পরস্পর পরিমেয় নয়—বাহু পূর্ণ সংখ্যায় পরিমেয় হলে কর্ণ পরিমেয় হবে না, আবার কর্ণ পরিমেয় হলে বাহু হবে না। বর্গের বাহু যদি ১ হয়, তার কর্ণ হয় ২-এর বর্গমূল, এবং ১ যেহেতু পরিমেয়, ২-এর বর্গমূল কখনো চূড়ান্ত পরিমেয় নয়। একে দুটি পূর্ণ সংখ্যার কোনো অনুপাতে প্রকাশ করা যায় না। এটি একেবারেই নতুন ধরণের সংখ্যা, মহান পীথাগোরাস! "

গভীর নিঃস্তব্ধতা নেমে আসে সেমিসার্কেলে। আইওনিয়ান সাগর থেকে পাক খেতে খেতে সাদা কুয়াশা ছড়িয়ে পরে ভুখণ্ডে, শীতলতর হয় ভূমধ্যসাগরীয় রাত। হিপ্যাসাসের যুক্তি বুঝতে পেরেছেন তিনি, কিন্তু এখনই সামলে নেয়া প্রয়োজন ব্যাপারটি, নয়তো ভ্রাতৃগোষ্ঠির ভাঙন ঠেকাতে পারবে না কেউ!
"তুমি অশুভ অযৌক্তিক (irrational) এক সংখ্যার কথা বললে, হিপ্যাসাস। আমি আরো পরীক্ষা করে দেখব তোমার প্রমাণ, তবে উদ্ধত, অমার্জিত আচরণের প্রায়শ্চিত্ত করতে হবে তোমাকে। আগামীকাল প্রত্যূষেই জাহাজে করে ক্রোটন ত্যাগ করবে তুমি, আমার নির্দেশ না পাওয়া পর্যন্ত মেটাপানটাম আসার চেষ্টা করবে না এবং কোথাও প্রকাশও করবে না অশুভ সংখ্যাটির কথা।" সভা ত্যাগ করেন পীথাগোরাস।
_________________
"এ-ই হচ্ছে হিপ্যাসাসের গল্প, ভয়ঙ্কর অমূলদ সংখ্যার জন্মের গল্প।" বিবর্ণ পোশাক পরিহিত মানুষটি, চোখে তার অপার্থিব আনন্দ-আভা, চারপাশে মানুষের ভীড়, বলতে লাগল। দীনহীন এক চারণকবি সে—পথে-প্রান্তরে বর্ণনা করে গণিতের উপাখ্যান, গণিতই মহান গীতিকবিতা তার কাছে, আনন্দ-বেদনা হাসি-কান্নার গৌরবগাঁথা।
"সহজ-সরল ভাষায় নিজের মতো করে এ উপাখ্যান বর্ণনা করার চেষ্টা করেছি; এতে আছে ইতিহাস, আছে কিংবদন্তি, পুরাকালের পরম কথা, যার সত্য-মিথ্যা আজ হারিয়ে গেছে কালের গর্ভে। মানুষ হিসেবে আমারও রয়েছে সীমাবদ্ধতা, ভুল-ত্রুটি নিজ গুণে মার্জনা করবেন।" দু'হাত জোড় করে বুকের কাছে রাখে সে।
"হিপ্যাসাসের শেষ পর্যন্ত কী হলো!" উৎসুক জনতা জানতে চায়।
"গুরুর আদেশে পরদিনই সমুদ্রযাত্রা করে সে। তারপর হঠাৎই হারিয়ে যায় ভূমধ্যসাগরের বুকে, কেউ তাকে আর দেখেনি কোনো দিন! শান্ত মাছরাঙা দিন [halcyon days] ছিল সেদিন, কিন্তু কেউ বলে ঝড়ে ভেসে গেছে সে, কেউ বলে ভ্রাতৃগোষ্ঠির সদস্যরা খুন করে লাশ তার ফেলে দিয়েছে সাগরে।"

"শান্তি পাক হিপ্যাসাসের আত্মা, সুখে থাকুক জগতের সব মানুষ।" মাটি থেকে কাপড়ের ঝোলাটি তুলে নেয় চারণকবি, জনপদটি পেছনে ফেলে দিগন্তজোড়া সবুজ মাঠে নেমে পড়ে সে, এগিয়ে যেতে থাকে নতুন আরেক জনপথের সন্ধানে, যারা গণিতের প্রতি ভালোবাসা মমতায় তাকে থামিয়ে দেবে চলার পথে, গভীর আগ্রহে শুনতে চাইবে প্রাচীন মানুষদের কথা— জ্ঞানের মধ্যেই যারা খুঁজে পেয়েছেন জীবনের মহত্তম অর্থ, পরিশুদ্ধতম আনন্দ।